© Pint of Science, 2026. All rights reserved.
Shakespeare, igual que cualquiera que haya ido a la playa, sabía que «suave fluye el agua cuando el cauce es hondo». De la misma manera, si alguien nos preguntase dónde rompen las olas, todos responderíamos que cerca de la orilla. Ahora vamos a intentar explicar un poco de las matemáticas detrás de este fenómeno.
No suele haber muchas cosas entre un matemático que estudia mecánica de fluidos y Kelly Slater, el surfista once veces campeón del mundo (¡y actor secundario en la serie de televisión «Los vigilantes de la playa»!). Sin embargo, para sorpresa de muchos, Slater afirmó que gran parte de su éxito se debía a sus conocimientos sobre las olas en el mar. Ese interés en el comportamiento de las olas es algo que une a Slater con el gremio del que formo parte y, ¿por qué no?, ¡hasta con el mismísimo Leonhard Euler!.
El lector exigente estará pensando que si bien Slater tiene un conocimiento eminentemente práctico con unas pinceladas, quizá, de física rudimentaria, los matemáticos, que trabajamos con objetos abstractos, sólo tenemos un conocimiento sobre modelos. Lo cierto es que al que piense eso no le falta razón (y de hecho desde ahora sólo vamos a hablar de modelos matemáticos y de su comportamiento), sin embargo tendrá que estar de acuerdo conmigo en que las matemáticas son irracionalmente precisas describiendo fenómenos físicos. En particular, deberíamos poder recuperar con nuestro modelo matemático el hecho de que las olas rompen más fácilmente cuando el agua es poco profunda. Al proceso de recuperar fenómenos naturales desde los modelos matemáticos se le llama en ocasiones validación del modelo. Y, si uno lo piensa bien, es algo bastante importante. Al fin y al cabo, los aviones o barcos en los que nos subimos están diseñados usando un modelo matemático que, decimos, se parece a la realidad física. Así que, ¿dónde queda el diseño de nuestros barcos si el modelo matemático falla en reflejar algo tan básico como que las olas rompen cerca de la arena?

El modelo matemático básico de un fluido debe describir tanto la velocidad que tienen las partículas de agua como las fuerzas internas a las que están sometidas. Así, para cada punto del espacio ocupado por el agua, el modelo posee cuatro incógnitas, tres se corresponden con un vector del campo de velocidades y la cuarta describe la fuerza con la que unas partículas empujan a otras al moverse. Esta fuerza recibe el nombre de presión.
En ocasiones, como por ejemplo cuando se estudian olas en el mar, el lugar del espacio donde está el fluido cambia con el tiempo (debido a que la ola se mueve) y la superficie que separa el fluido del aire se convierte en una incógnita añadida al modelo. Esta nueva incógnita recibe el nombre de frontera libre (frontera porque es el límite de la región ocupada por el agua y libre porque el modelo le permite moverse). Por lo tanto, en el caso concreto de las olas del mar, tenemos un modelo con cinco incógnitas, las tres coordenadas de los vectores de velocidad, la presión y la frontera libre.
Para resolver estas cinco incógnitas tenemos un conjunto de cinco ecuaciones diferenciales que reciben el nombre de ecuaciones de Navier-Stokes incompresibles con frontera libre. Tres de ellas se corresponden con la Segunda Ley de Newton (F=ma), la cuarta refleja que el campo de velocidades es incompresible, es decir, que el volumen de fluido se conserva y finalmente, la quinta ecuación impone que la ola es transportada por el agua.
Los lectores familiarizados con los llamados problemas del milenio del Instituto Clay de Matemáticas habrán reconocido en las ecuaciones de Navier-Stokes uno de los desafíos cuya solución se premia con un millón de dólares estadounidenses. Sin embargo, en el enunciado del problema relativo a estas ecuaciones, se especifica que la región ocupada por el fluido está fija. Es decir, que nuestra motivación de las olas en el mar no cuenta para ganar el millón. Pero sigamos, al fin y al cabo, uno no estudia matemáticas para hacerse rico...
Una vez que el problema del milenio queda descartado podemos introducir alguna hipótesis en las ecuaciones (que dejarán entonces de recibir el nombre de Navier-Stokes) que simplifique nuestro análisis. Así vamos a asumir que estamos interesados en las olas en una bahía con forma de «U» mayúscula, siendo esta «U» muy estrecha y muy larga y donde el agua fluye con muy poca aceleración. De esta manera, la proximidad de las orillas paralelas nos permite simplificar las tres ecuaciones de Navier-Stokes hasta conseguir un nuevo juego de dos ecuaciones que reciben el nombre de Ley de Darcy o de Hele-Shaw. Estas ecuaciones también aparecen en fluidos moviéndose en un medio poroso, por ejemplo, agua y petróleo en un pozo petrolífero. Con estas hipótesis añadidas las olas son simétricas y pueden ser descritas con sólo dos variables. Es este nuevo conjunto de ecuaciones el que vamos a estudiar.
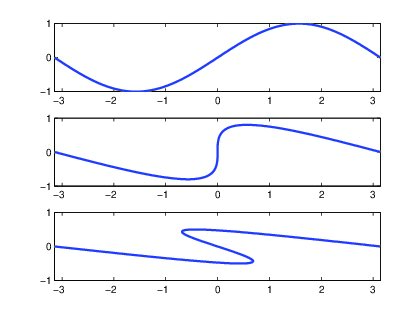
Siguiendo el determinismo newtoniano, tenemos que, dada una ola, Z, en el instante inicial t=0, esta ola se mueve dando lugar a una única ola en el instante t=1 y, a su vez, la ola Z viene de una única ola en el instante t=-1.
Fijemos un punto en el espacio, por ejemplo, el origen. Si queremos probar matemáticamente que las olas de nuestro modelo matemático rompen, tenemos que conseguir una ola inicial Z cuyo vector tangente en el origen sea perpendicular al suelo (es decir, su primera coordenada sea exactamente cero) y tal que, A tenga un vector tangente (en el origen) con primera coordenada positiva mientras que D tenga un vector tangente (de nuevo, en el origen) con primera coordenada negativa. Esta nueva formulación del problema nos permite reducir el fenómeno «la ola rompe a tiempo t=0» a «la derivada temporal de la primera coordenada del vector tangente (en el origen) es negativa».
¡Estamos de suerte! este segundo problema es algo a lo que estamos acostumbrados casi desde el instituto y se puede resolver . Sin embargo, nuestro objetivo no era conseguir probar matemáticamente que las olas rompen según el modelo, ¡nosotros queríamos probar que la profundidad juega un papel crucial en esto!.
Para nuestra tarea necesitamos una ola inicial Z, tal que si la profundidad es finita haga lo que hemos descrito anteriormente mientras que si la profundidad es infinita (es decir, la ola Z está lejos de la orilla), el vector tangente en el origen a la ola D tenga primera coordenada positiva. Para poder probar esa diferencia de signos necesitamos calcular buenas estimaciones del valor real usando un ordenador. Sin embargo, al usar el ordenador, necesitamos estar seguros de los errores que el ordenador comete tanto por la representación de los números como por el algoritmo empleado. Esto puede hacerse usando aritmética de intervalos. ¡De esta manera conseguimos lo que se conoce como una prueba matemática asistida por ordenador del efecto de la profundidad en que las olas rompan!

Si bien las matemáticas actuales están lejos de ser de mucha ayuda si Slater intenta conquistar su duodécimo campeonato, nuestra comprensión de los modelos matemáticos que aparecen en el estudio de los fluidos es mucho mayor que hace unos pocos años.
Texto: Rafael Granero Belinchón (Assistant Professor - Dep. of Mathematics, Statistics and Computer Science - Universidad de Cantabria)




